Soal dan Kunci Jawaban Matematika Kelas 8 SMP/MTS Halaman 144-147

Soal dan Kunci Jawaban Matematika Kelas 8 –Yuk simak, pada pertemuan kali kami akan membahasa mengenai Kunci Jawaban SOAL Matematika Kelas 8 SMP MTS Halaman 144-147 Ayo Berlatih 8.2 Luas Permukaan Prisma, secara lengkap untuk kalian. Soal dan kunci jawaban ini di buat untuk bahan latihan kalian agar lebih siap dengan proses pembelajaran di sekolah. Soal dan kunci jawaban dan juga Artikel ini dibuat untuk membantu adik-adik memahami pembelajaran serta menjawab pertanyaan secara mandiri di rumah. Soal dan kunci jawaban ini juga tidak menjamin kebenaran yang bersifat mutlak karena tidak menutup kemungkinan ada eksplorasi jawaban lainnya.

Berikut Soal dan Kunci Jawaban Matematika Kelas 8 SMP MTS Halaman 144-147 Ayo Berlatih 8.2 Luas Permukaan Prisma.

 

1. Sebuah prisma alasnya berbentuk persegi panjang dengan luas alas 40cm2. jika lebar persegi panjang 5cm dan tinggi prisma 12cm, hitunglah luas permukaan prisma?

 

Jawaban dan Pembahasan 

 

Diketahui :

– Luas Alas (La) = 40 cm²
– Lebar Alas (l) = 5 cm
– Tinggi Prisma (t) = 12 cm

Ditanya :

– Luas Permukaan Prisma (Lp) = ……?

 

Penyelesaian :

– Panjang Alas (p) :

La = p × l
p = La ÷ l
p = 40 ÷ 5
p = 8 cm

– Luas Permukaan Prisma (Lp) :

Lp = 2La + 2pt + 2lt
Lp = (2(40)) + 2(8)(12) + 2(5)(12)
Lp = 80 + 16(12) + 10(12)
Lp = 80 + 192 + 120
Lp = 272 + 120
Lp = 392 cm²

 

 

2. Alas sebuah prisma berbentuk segitiga siku-siku dengan panjang sisi 12 cm, 9 cm, dan 15 cm. Jika tinggi prisma adalah 30 cm, hitunglah luas permukaan prisma tersebut.

 

Jawaban dan Pembahasan 

 

Luas prima = keliling alas x tinggi prisma + 2 x luas alas
lp = (9+12+15) x 30 + 2 x 1/2 x 9 x 12
lp = 36 x 30 + 108
lp= 1.188 cm²

 

 

3. Pernahkah kalian berkemah?

Berbentuk apakah tenda yang kamu pakai? Bila tenda yang kamu pakai seperti gambar tenda di samping, dapatkah kamu menghitung luas kain terkecil yang diperlukan untuk membuat tenda itu? Coba hitunglah.

 

Jawaban dan Pembahasan 

 

Pada bagian depan tenda berbentuk segitiga sama kaki yang tergambar pada Δ ABC.

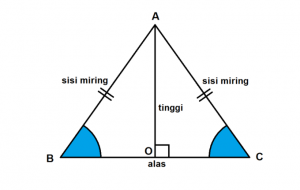
Untuk mengitung panjang kain yang bewarna hijau, kita menggunakan pythagoras.

BC² = t² + (AB/2)²
= 2² + ()²
= 4 +
= 4 + 2,25
= 6,25
BC = √6,25
BC = 2,5 m

Panjang kain warna hijau = 2 × 2,5 m
= 5 m
Menentukan luas kain minimal pada tenda
Luas kain = (2 × luas segitiga) + (luas kain warna hijau)
= (2 × 1/2 × 3 × 2 m²) + (5 × 4 m²)
= 6 m² + 20 m²
= 26 m²

Jadi luas kain minimal pada tenda tersebut adalah 26 m²

 

 

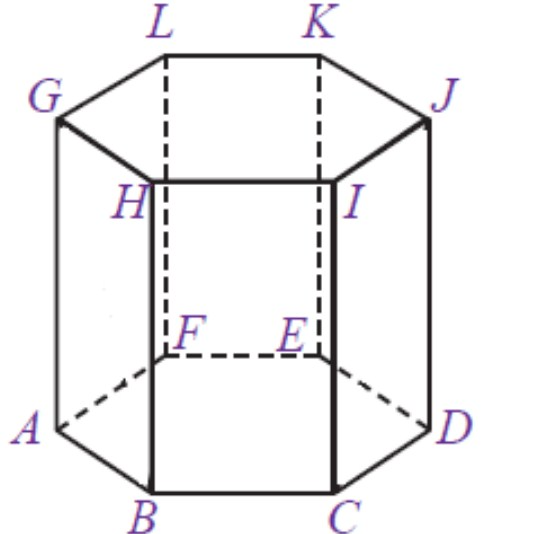
4. Sebuah prisma tegak segienam beraturan ABCDEF.GHIJKL mempunyai panjang rusuk alas 10 cm dan panjang rusuk tegak 80 cm.

a. Gambarlah bangun prismanya.
b. Tentukan luas bidang tegaknya.
c. Tentukan luas permukaan prisma.

 

Jawaban dan Pembahasan 

 

Perhatikan gambar

gambar prisma segi enam

B. Luas bidang tegak = Keliling alas x tinggi prisma
= 6 × sisi × tinggi prisma
= 6 × 10 cm × 80 cm
= 4800 cm²

Jadi, luas bidang tegak adalah 4800 cm

C. Segienam dari alas prisma terdiri dari 6 segitiga sama sisi yang kongruen atau sama besar. cari tinggi segitiga dengan menggunakan teorema phytagoras:

Kunci Jawaban SOAL Matematika Kelas 8 SMP MTS Halaman 144-147 Ayo Berlatih 8.2 Luas Permukaan Prisma, Lengkap

(tΔ)² = 10² – 5²
(tΔ)² = 100 – 25
(tΔ)² = 75
tΔ = √75
tΔ = √(25×3)
tΔ = 5√3 cm

Luas alas prisma (segienam) = 6 × Luas segitiga
= 6 × 1/2 × alas Δ × t Δ
= 3 × 10 cm × 5√3 cm
= 150√3 cm²

Luas permukaan prisma
= (2 × Luas alas ) + (Keliling alas × tinggi prisma)
= (2 × 150√3 cm²) + (6 × 10 cm × 80 cm)
= 300√3 cm² + 4800cm²
= (4800+300√3) cm²

Jadi, luas permukaan prisma adalah (4800+300√3) cm²

 

 

5. Sebuah prisma dengan alas berbentuk belah ketupat mempunyai panjang diagonal 24 cm dan 10 cm. Jika tinggi prisma 8 cm, maka luas permukaan prisma adalah ….

A. 768 cm2
B. 656 cm2
C. 536 cm2
D. 504 cm2

 

Jawaban dan Pembahasan 

isi prrisma = 1/2 √d1²+d2²
= 1/2 √24²+10²
= 1/2 √576+100
= 1/2 √676
= 1/2 x 26
= 13 cm

Luas permukaan = 2 x L als + Keliling alas x tinggi
= 2 x 1/2 x d1 x d2 + 4s x t
= d1 x d2 + 4s x t
= 24 x 10 + 4 x 13 x 8
= 240 + 416
= 656 cm²

Jadi luasnya adalah 656 cm²

 

 

6. Indra akan membuat tiga buah papan nama dari kertas karton yang bagian kiri dan kanannya terbuka seperti tampak pada gambar.

Luas minimum karton yang diperlukan Indra adalah ….

A. 660 cm2
B. 700 cm2
C. 1.980 cm2
D. 2.100 cm2

 

Jawaban dan Pembahasan 

 

Diketahui

Tinggi prisma = 22 cm
Tinggi segitiga = 12 cm
Alas segitiga = 5 cm
Sisi miring = ?

Gunakan rumus prisma tanpa alas dan tutup
t(a + b + c)

Sebelumnya cari dulu sisi miringnya
s = √12² + 5²
s = √144 + 25
s = √169
s = 13
Jadi sisi miringnya 13 cm.
2(12 + 5 + 13)
22(30)
660 cm²
660 cm² × 3 = 1980 cm² (C).

 

 

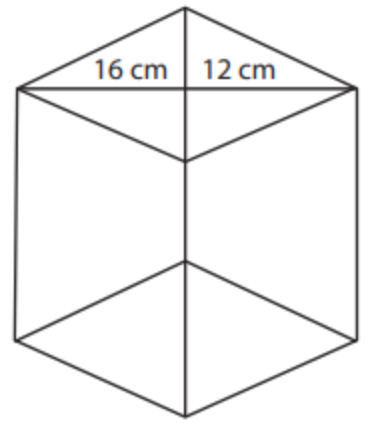
7. ABCD.EFGH pada gambar di samping

adalah prisma dengan ABFE sejajar DCGH jika panjang AB=4cm, BC=6cm,AE=8cm dan BF=5cm, maka luas permukaan prisma adalah…

 

Jawaban dan Pembahasan 

 

Bangun Ruang Prisma

AB= 4
BC = 6
AE = 8
BF = 5
EF = (√(8-5)²+(4²)= 5

Luas Permukaan = 2 ( luas trapesium ABFE) + Luas persegi panjang ADHE + Luas peresgipanjang BCGF + Luas persegipanjang ABCD + Luas persegi panjang EFGH

LP = 2{ 1/2 (BF+AE)(AB)) + (AD xAE) + (BC xBF) + (ABxBC) + (EFxFG)
LP = (5+8)(4) + (6×8) + (6×5) + (4 x 6) + (5 x 6)
LP= 52 + 48 + 30+ 24 + 30
LP = 184 cm²

 

 

8. Sebuah prisma alasnya berbentuk belah ketupat dengan panjang diagonal 16cm dan 12 cm . tentukan tinggi prisma jika luas permukaannya adalah 672 cm2

Jawaban dan Pembahasan 

 

Diketahui :

d1 = 16 cm
d2 = 12 cm

luas permukaan = 672 cm²

Dijawab :

luas alas = 1/2 . d1 . d2
= 1/2 . 16 . 12
= 96 cm²

sisi belah ketupat (s) = √(1/2 . d1)² +(1/2 . d2)²
= √(1/2 . 16)² +(1/2 . 12)²
= √8² +6²
= √100
= 10 cm

Keliling = 4s
= 4(10)
= 40 cm

Luas permukaan = (2 x luas alas) +(keiling x tinggi)
672 = 2(96) +(40 x t)
672 = 192 +40t
672 -192 = 40t
480 = 40t
t = 480/40
t = 12 cm

 

 

Nah demikian pembahasan Soal dan Kunci Jawaban Matematika Kelas 8 SMP/MTS Halaman 144-147. Semoga bisa membantu proses belajar kalian ya, Terima kasih.